「数据结构与算法」红黑树（Red-Black Tree）

数据结构
留言

平衡二叉查找树其实有很多，比如，红黑树（Red-Black Tree，简称 R-B Tree）、伸展树（Splay Tree）、树堆（Treap）等，但是我们提到平衡二叉查找树，听到的基本都是红黑树，它是一种不严格的平衡二叉查找树。
红黑树是一种含有红黑节点并能自平衡的二叉查找树。它必须满足下面性质：

  1. 每个节点要么是红色，要么是黑色；
  2. 根节点是黑色的；
  3. 每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存储数据；
  4. 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的；
  5. 任意一节点到每个叶子节点的路径，都包含相同数目的黑色节点；

1. 红黑树的平衡特征

红黑树与AVL树类似，都在添加和删除的时候通过旋转操作保持二叉树的平衡，以求更高效的查询性能。

红黑树牺牲了部分平衡性，以换取插入/删除操作时较少的旋转操作，整体来说性能要优于AVL树。

红黑树的黑色属性（即性质第五点）：任意一节点到每个叶子节点的路径，都包含相同数目的黑色节点。
黑色属性，可以理解为平衡特征， 如果满足不了平衡特征，就要进行平衡操作（变色、左旋、右旋）。

红黑树的平衡条件，是以黑色节点的高度来约束的，所以称红黑树这种平衡为黑色完美平衡。

如下图，去掉红色节点，会得到一个四叉树， 从根节点到每一个叶子节点高度相同，就是红黑树的根节点到叶子的黑色路径长度。

2. 红黑树的平衡调整

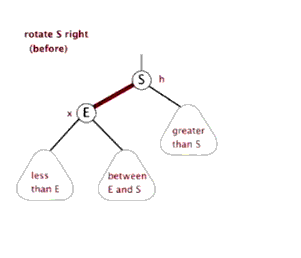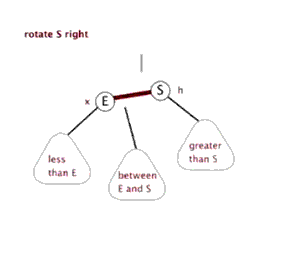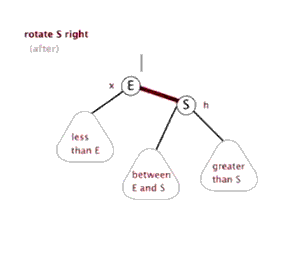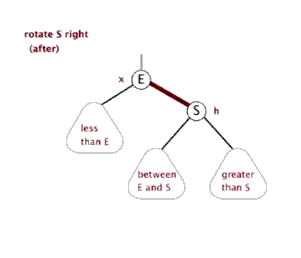
三种操作：左旋（rotate left）、右旋（rotate right）和 变色。

  • 左旋，即是逆时针旋转，以某个节点作为旋转点，其右子节点变为旋转节点的父节点，右子节点的左子节点变为旋转节点的右子节点，左子节点保持不变；

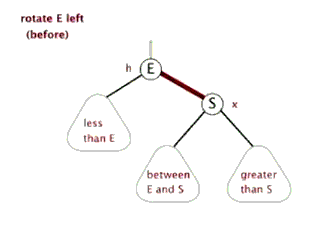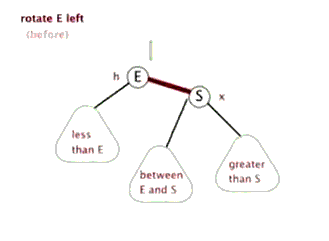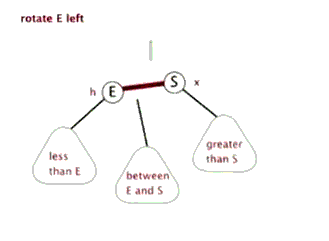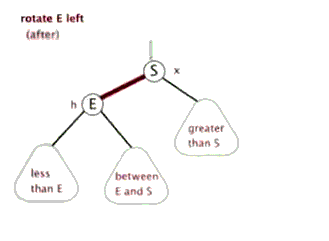
  • 右旋，即是顺时针旋转，以某个节点作为旋转点，其左子节点变为旋转节点的父节点，左子节点的右子节点变为旋转节点的左子节点，右子节点保持不变。

  • 变色，节点的颜色由红变黑或由黑变红；

3. 插入操作的平衡调整

红黑树规定，插入的节点一定是红色的。而且，二叉查找树中新插入的节点都是放在叶子节点上。

红黑树的平衡调整过程是一个迭代的过程。
我们把正在处理的节点叫做关注节点。关注节点会随着不停地迭代处理，而不断发生变化。最开始的关注节点就是新插入的节点。

  1. 新插入节点的父节点是黑色的，红黑树不需要调整。

  2. 新插入节点是根节点，根节点变黑即可。

  3. 新插入节点的父节点和它的叔叔都是红色，红黑树只需要变色，不需要旋转。

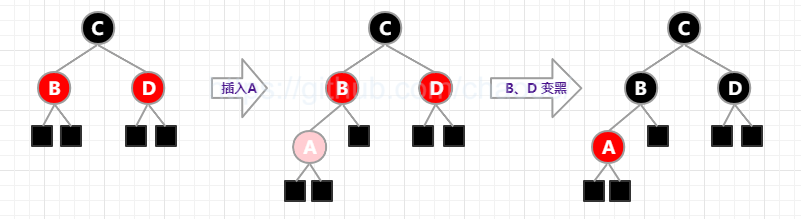
  4. 新插入节点的父节点是红色，但它叔叔是黑色（可能为null的黑色空节点），红黑树需要变色+旋转。

需要红黑树变色+旋转（父节点红色，叔节点黑色）的四种情形：

  • 一、LL型（左左插），即父节点和插入的节点都是左节点：

    • ①父节点变黑色，爷节点变红色
    • ②爷节点右旋

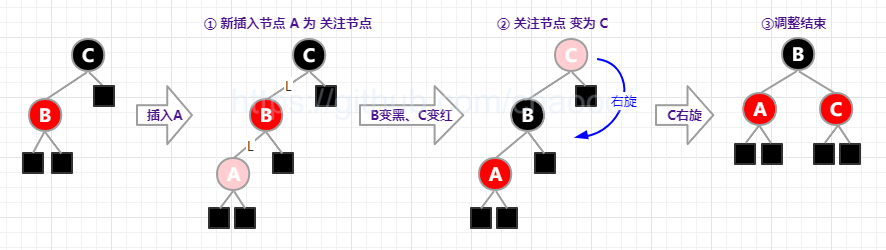
  • 二、LR型（左右插），即父节点是左节点，插入节点是右节点：

    • ①父节点左旋，父子交换变成了【情形一·LL】
    • ②跳到【LL型】的调整

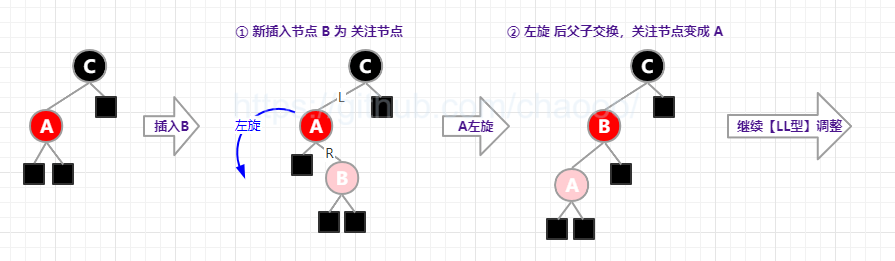
  • 三、RR型（右右插），即父节点和插入的节点都是右节点：

    • ①父节点变黑色，爷节点变红色
    • ②爷节点左旋

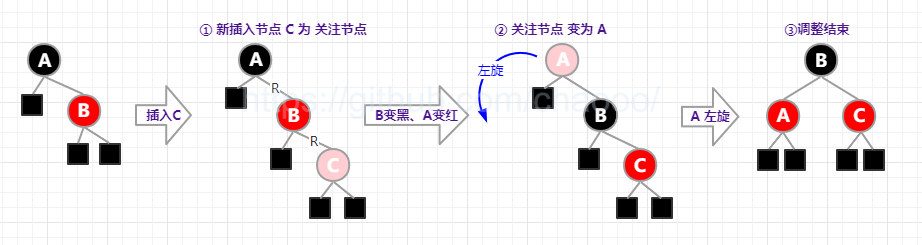
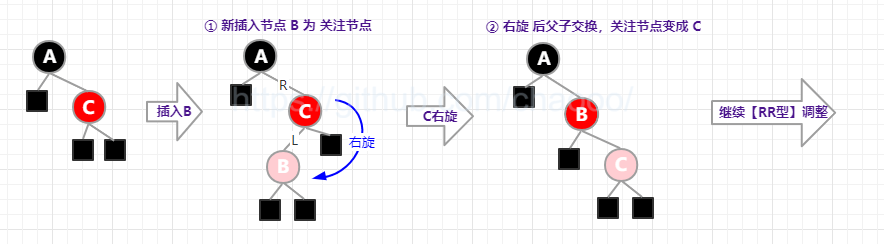
  • 二、RL型（右左插），即父节点是右节点，插入的节点是左节点：

    • ①父节点右旋，父子交换变成了【情形三·RR】
    • ②跳到【RR型】的调整

4. 删除操作的平衡调整

红黑树的删除情况相对插入会复杂一些，不过原理都是类似的。

4.1 二叉查找树的删除操作

  1. 待删除节点没有子节点，将父节点中，指向要删除节点的指针置为null。
  2. 待删除节点只有一个子节点，更新父节点中，指向要删除节点的指针，让它指向要删除节点的子节点。
  3. 待删除节点有两个子节点，用后继节点或者前继节点替换删除节点，然后再删除掉替换节点。
    • 后继节点：删除节点的右子树中的最小节点，即右子树中最左节点。
    • 前继节点：删除节点的左子树中最大节点，即左子树中最右节点。

4.2 红黑树的删除动作

红黑树和二叉查找树的删除类似，只不过加上颜色属性（这里的子节点均指非黑色叶子NULL节点）：

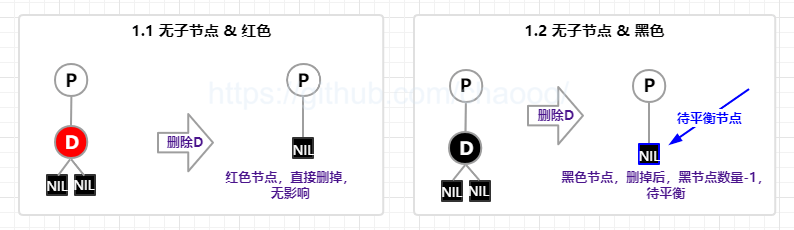
  1. 无子节点时，删除节点可能为红色或者黑色；

    • 1.1 如果为红色，直接删除即可，不会影响黑色节点的数量；
    • 1.2 如果为黑色，则需要进行删除平衡的操作（如果是根节点，无需平衡操作）；

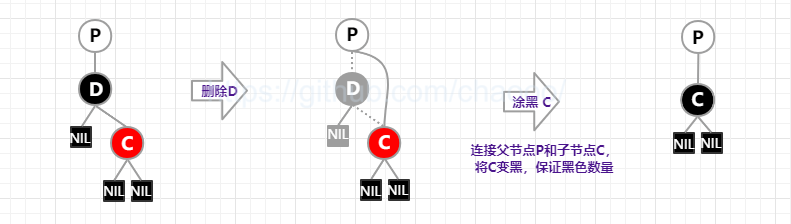
  2. 只有一个子节点时，删除节点只能是黑色，其子节点是红色（否则无法满足红黑树的性质）。 此时用删除节点的子节点接到父节点，且将子节点颜色涂黑，保证黑色数量。

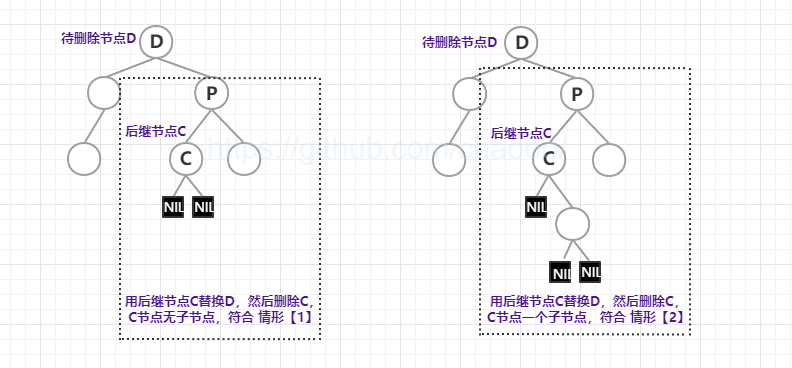
  3. 有两个子节点时，与二叉搜索树一样，使用后继节点作为替换的删除节点，情形转至为【1】或【2】处理。

删除情形【3】总是会转换为情形【1】或【2】的，
而情形【1.2】（删除节点无子节点且是黑色）还需要额外的平衡调整；
因为一旦该节点被拿掉，红黑树中通过该节点的路径黑色节点数量将会减1，而且无法像情形【2】那样将子节点涂黑来达到平衡。此时只能自底向上进行平衡操作。

4.3 红黑树删除后的平衡操作

为了简化描述，先约定关注节点及相关节点的名称：

【情形 1.1】： 兄黑（S 黑），兄子全黑（L 和 R 全黑），父红（P 红）；

即 兄弟节点为黑色，兄弟节点的子节点全部黑色，父节点为红色。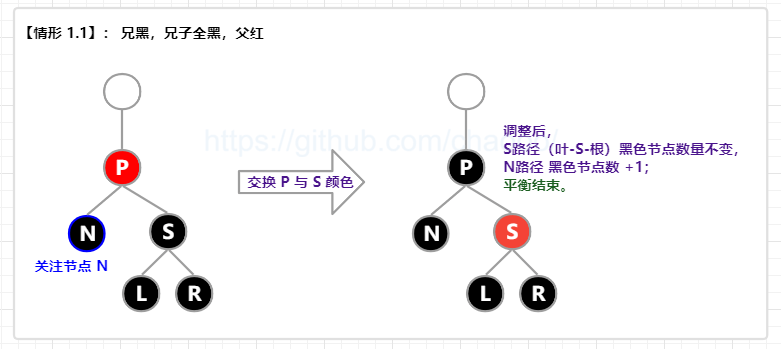

【情形 1.2】： 兄黑（S 黑），兄子全黑（L 和 R 全黑），父黑（P 黑）；

即 兄弟节点为黑色，兄弟节点的子节点全部黑色，父节点为黑色。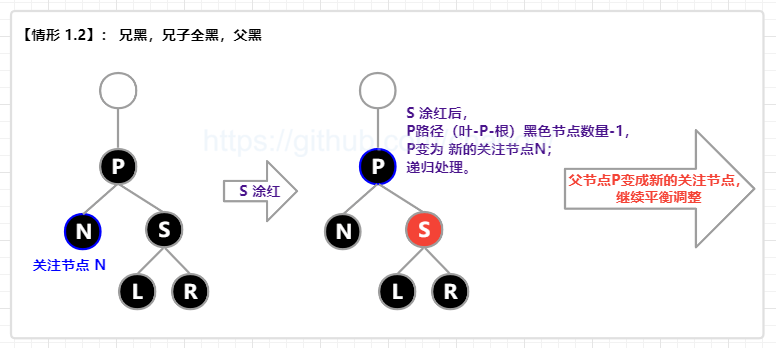

【情形 2.1】： 兄黑（S 黑），兄在左（S 左），兄左子红（L 红）；

即 兄弟节点为黑色，且兄弟节点在左边，兄弟节点的左子节点为红色。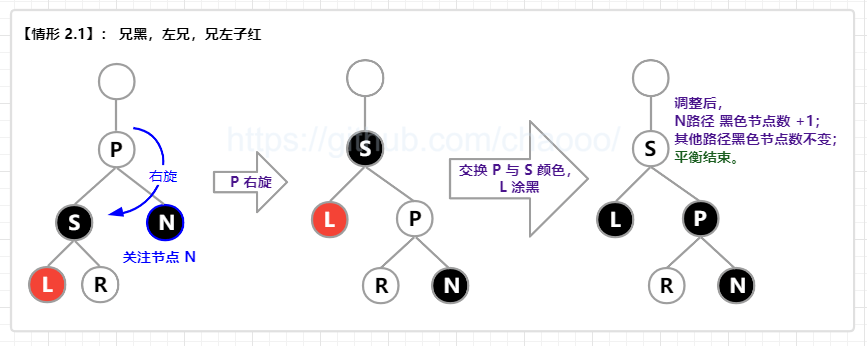

【情形 2.2】： 兄黑（S 黑），兄在左（S 左），兄左子黑（L 黑）；

即 兄弟节点为黑色，且兄弟节点在左边，兄弟节点的左子节点为黑色。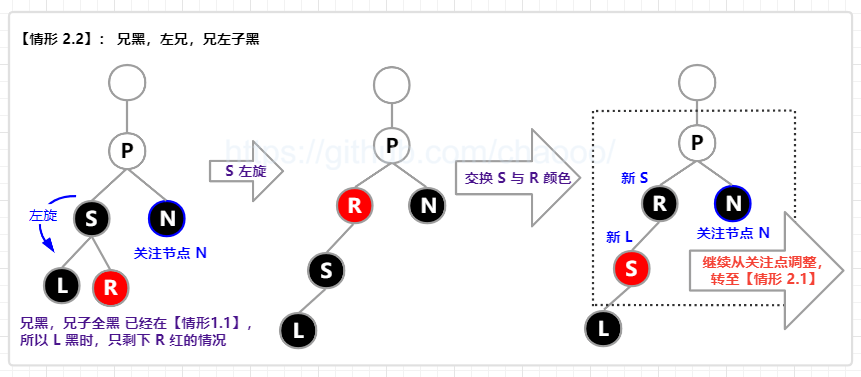

【情形 2.3】： 兄黑（S 黑），兄在右（S 右），兄右子红（R 红）；

即 兄弟节点为黑色，且兄弟节点在右边，兄弟节点的右子节点为红色。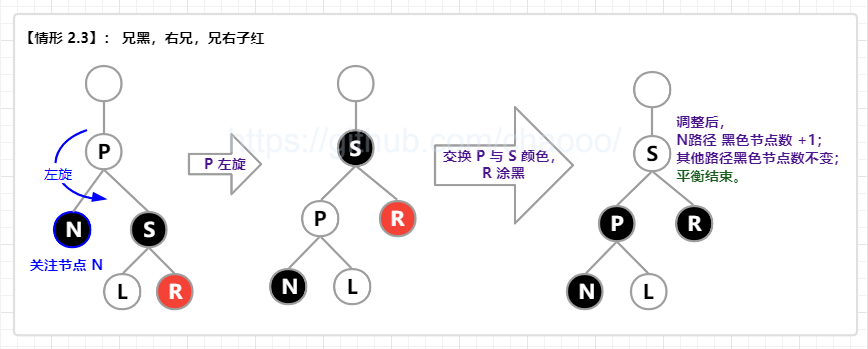

【情形 2.4】： 兄黑（S 黑），兄在右（S 右），兄右子黑（R 黑）；

即 兄弟节点为黑色，且兄弟节点在右边，兄弟节点的右子节点为黑色。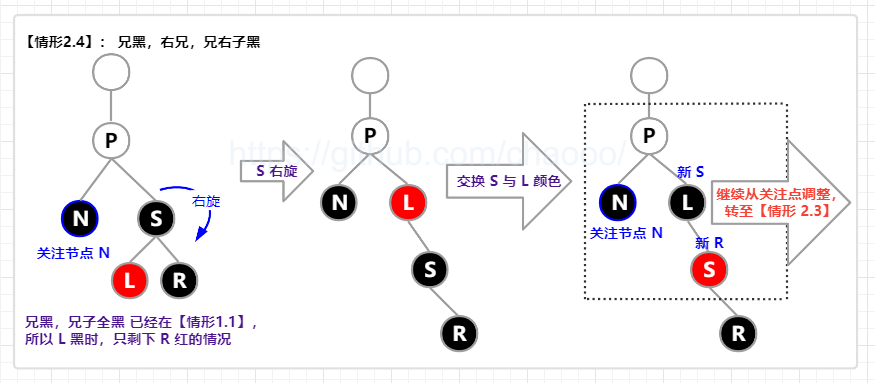

【情形 3.1】： 兄红（S 红），兄在左（S 左）；

即 兄弟节点为红色，且兄弟节点在左边。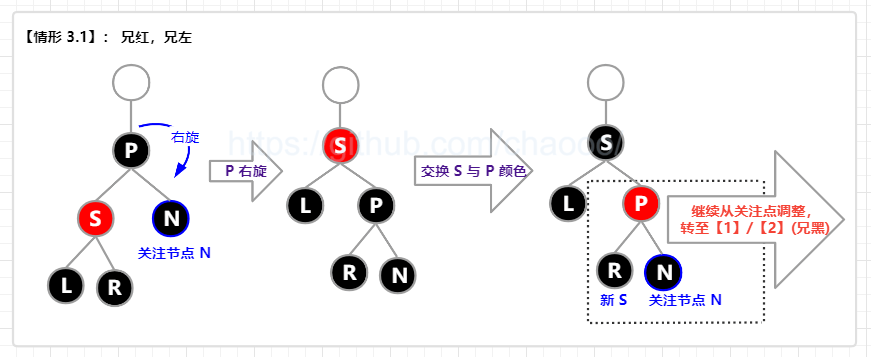

【情形 3.2】： 兄红（S 红），兄在右（S 右）；

即 兄弟节点为红色，且兄弟节点在右边。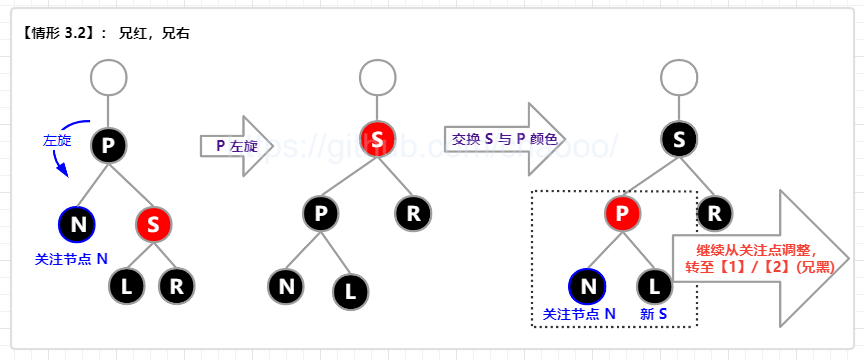

4.4 红黑树删除总结

删除动作（移除节点）之后，若待平衡节点是黑色的叶子节点：
平衡调整情形，主要根据 [兄节点的位置/颜色]、[兄的子节点的颜色]、[父节点颜色] 进行分类：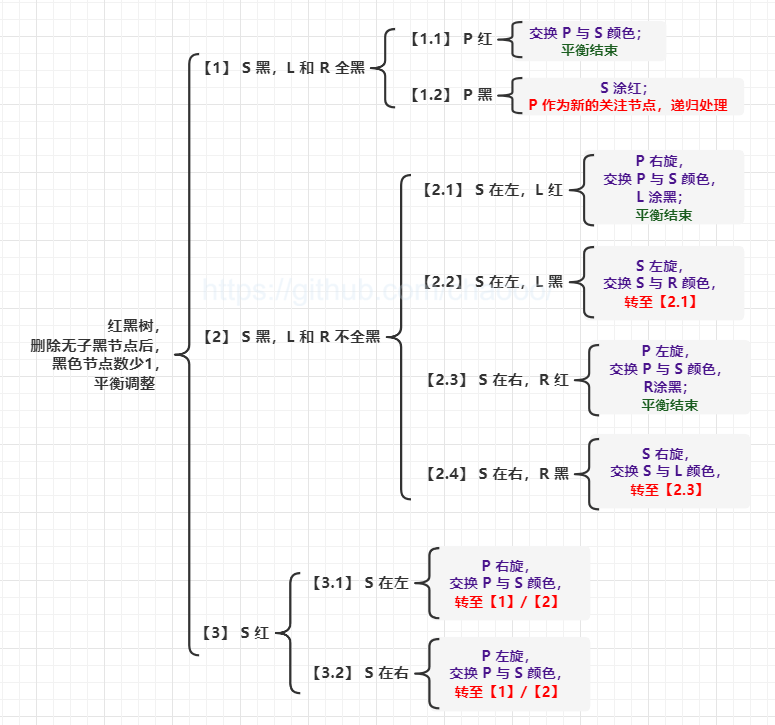

5. 红黑树的应用场景

二叉查找树的时间复杂度会受到其树深度的影响，而红黑树可以保证在最坏情况下的时间复杂度仍为O(lgn)。
当数据量多到一定程度时，使用红黑树比二叉查找树的效率要高。

平衡二叉树的时间复杂度是O(logn)，红黑树的时间复杂度为O(lgn)，两者都表示的都是时间复杂度为对数关系（lg 函数为底是 10 的对数）。

同平衡二叉树相比较，红黑树没有像平衡二叉树对平衡性要求的那么苛刻，虽然两者的时间复杂度相同，但是红黑树在实际测算中的速度要更胜一筹！

红黑树的使用非常广泛，

  • 如Java的TreeMap和TreeSet都是基于红黑树实现的（相对与HashMap优势，内部key保持有序，且支持自定义排序比较器）；
  • 而JDK8中HashMap当链表长度大于8时也会转化为红黑树（时间复杂度从O(n)-->O(lgn) ，且自旋开销比其他树低）。
  • 其他：如epoll在内核中的实现，用红黑树管理事件块（文件描述符）；linux进程调度Completely Fair Scheduler，用红黑树管理进程控制块；nginx中，用红黑树管理timer等。