「数据结构与算法」堆（Heap）

2022年05月02日

堆的两点要求：

堆是一个完全二叉树；
堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值。
- 对于每个节点的值都大于等于子树中每个节点值的堆，我们叫做大顶堆。
- 对于每个节点的值都小于等于子树中每个节点值的堆，我们叫做小顶堆。

完全二叉树：除最后一层外，其他层的节点都满；并且最后一层的节点从左到右是连续排列，中间没有断开，空位都在右边。

在构建完全二叉树的时候，新加入的节点在最后一层从左往右依次排列，直到排满为止。

有两种方法存储一棵二叉树，一种是基于指针或者引用的二叉链式存储法，一种是基于数组的顺序存储法。
堆是一种完全二叉树，最常用的存储方式就是基于数组的顺序存储法。

1. 基于数组的顺序存储法。

如下图，我们把根节点存储在数组下标 i=1 的位置，那左子节点存储在下标 2*i = 2 的位置，右子节点存储在 2*i+1 = 3 的位置。以此类推，B节点的左子节点存储在 2*i = 2*2 = 4 的位置，右子节点存储在 2*i+1 = 2*2+1 = 5 的位置。

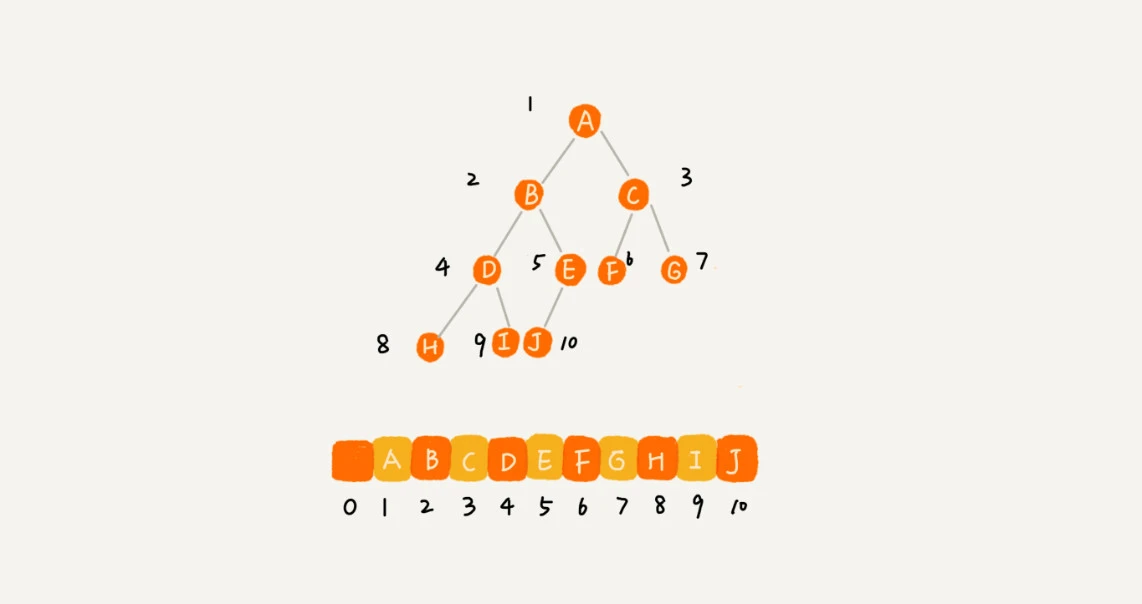
如果节点X存储在数组中下标为 i 的位置，下标为 2*i 的位置存储的就是左子节点，下标为 2*i+1 的位置存储的就是右子节点。
反过来，下标为 i/2 的位置存储就是它的父节点。
通过这种方式，我们只要知道根节点存储的位置（通常根节点会存储在下标为1的位置），这样就可以通过下标计算，把整棵树都串起来。

2. 堆化（heapify）

往堆中插入或者删除一个元素后，需要继续满足堆的两个特性，而这个重新维持堆特性的过程称为堆化（heapify）。

堆化非常简单，就是顺着节点所在的路径，向上或者向下，比较，然后交换。
堆化实际上有两种：从下往上、从上往下。

插入元素时涉及的是从下往上的堆化方法。
删除堆顶元素涉及的是从上往下的堆化方法。

3. 往堆中插入一个元素

把新插入的元素放到堆的最后，需要继续满足堆的两个特性。

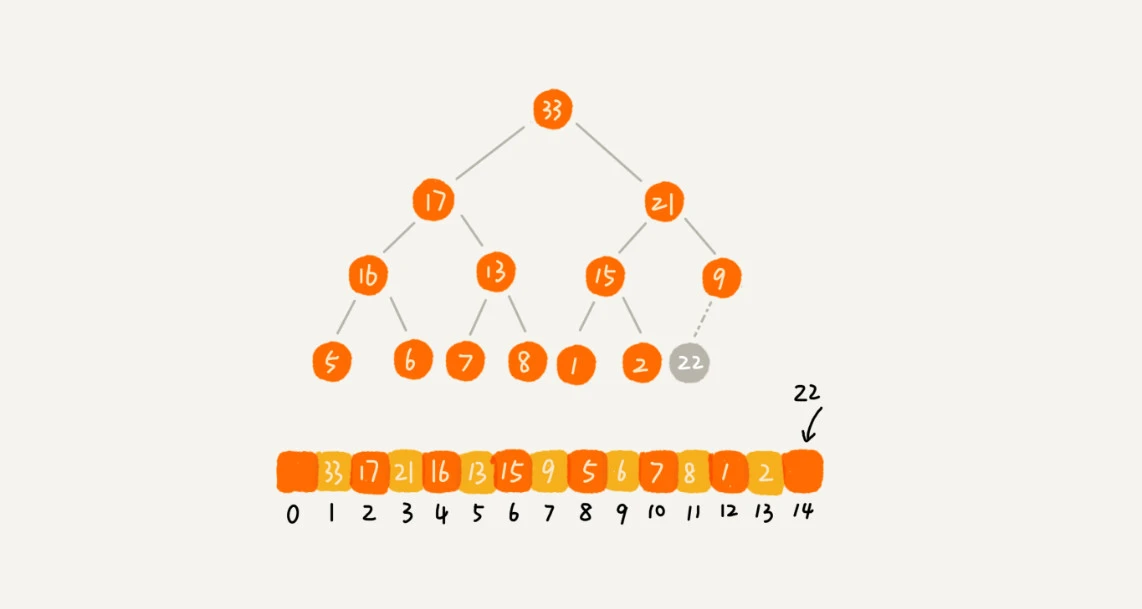
从下往上的堆化：
让新插入的节点与父节点对比大小。如果不满足子节点小于等于父节点的大小关系，我们就互换两个节点。
一直重复这个过程，直到父子节点之间满足刚说的那种大小关系。

往堆中插入数据的过程，翻译成代码：

public class Heap {
  private int[] a; // 数组，从下标1开始存储数据
  private int n;  // 堆可以存储的最大数据个数
  private int count; // 堆中已经存储的数据个数

  public Heap(int capacity) {
    a = new int[capacity + 1];
    n = capacity;
    count = 0;
  }

  public void insert(int data) {
    if (count >= n) return; // 堆满了
    ++count;
    a[count] = data;
    int i = count;
    while (i/2 > 0 && a[i] > a[i/2]) { // 自下往上堆化
      swap(a, i, i/2); // swap()函数作用：交换下标为i和i/2的两个元素
      i = i/2;
    }
  }
 }

4. 删除堆顶元素

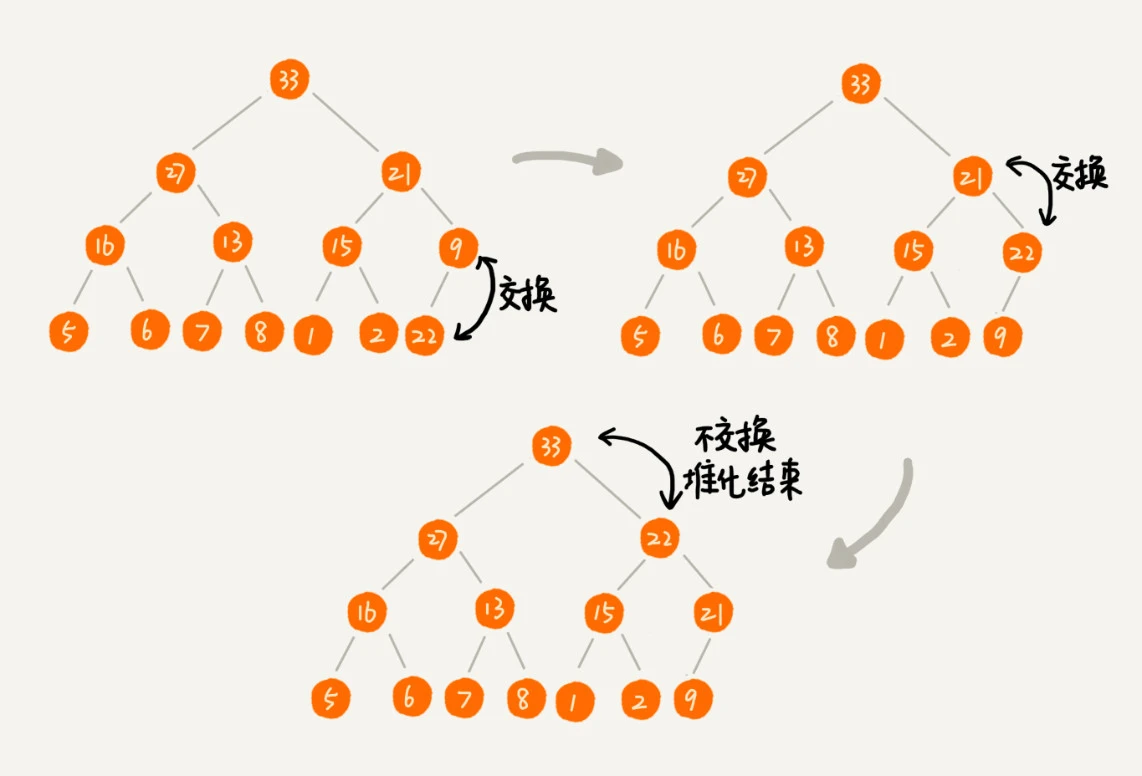
从堆的特性可以看出，堆顶元素存储的就是堆中数据的最大值或者最小值。
从上往下的堆化：
当我们删除堆顶元素之后，把最后一个节点放到堆顶，然后利用同样的父子节点对比方法。对于不满足父子节点大小关系的，互换两个节点，并且重复进行这个过程，直到父子节点之间满足大小关系为止。

堆顶元素删除的过程，翻译成代码：

public void removeMax() {
  if (count == 0) return -1; // 堆中没有数据
  a[1] = a[count];
  --count;
  heapify(a, count, 1);
}

private void heapify(int[] a, int n, int i) { // 自上往下堆化
  while (true) {
    int maxPos = i;
    if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;
    if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;
    if (maxPos == i) break;
    swap(a, i, maxPos);
    i = maxPos;
  }
}

2. 堆化的时间复杂度

一个包含 n 个节点的完全二叉树，树的高度不会超过 log2n。
堆化的过程是顺着节点所在路径比较交换的，所以堆化的时间复杂度跟树的高度成正比，也就是 O(logn)。
插入数据和删除堆顶元素的主要逻辑就是堆化，所以，往堆中插入一个元素和删除堆顶元素的时间复杂度都是 O(logn)。

3. 堆排序（heap sort）

堆排序（heap sort）是基于堆的一种排序，堆排序的过程大致分为两大步骤：建堆和排序。

大顶堆：每个节点的值都大于等于子树中每个节点值。
小顶堆：每个节点的值都小于等于子树中每个节点值。
求升序用大顶堆，求降序用小顶堆。

3.1 堆的构建

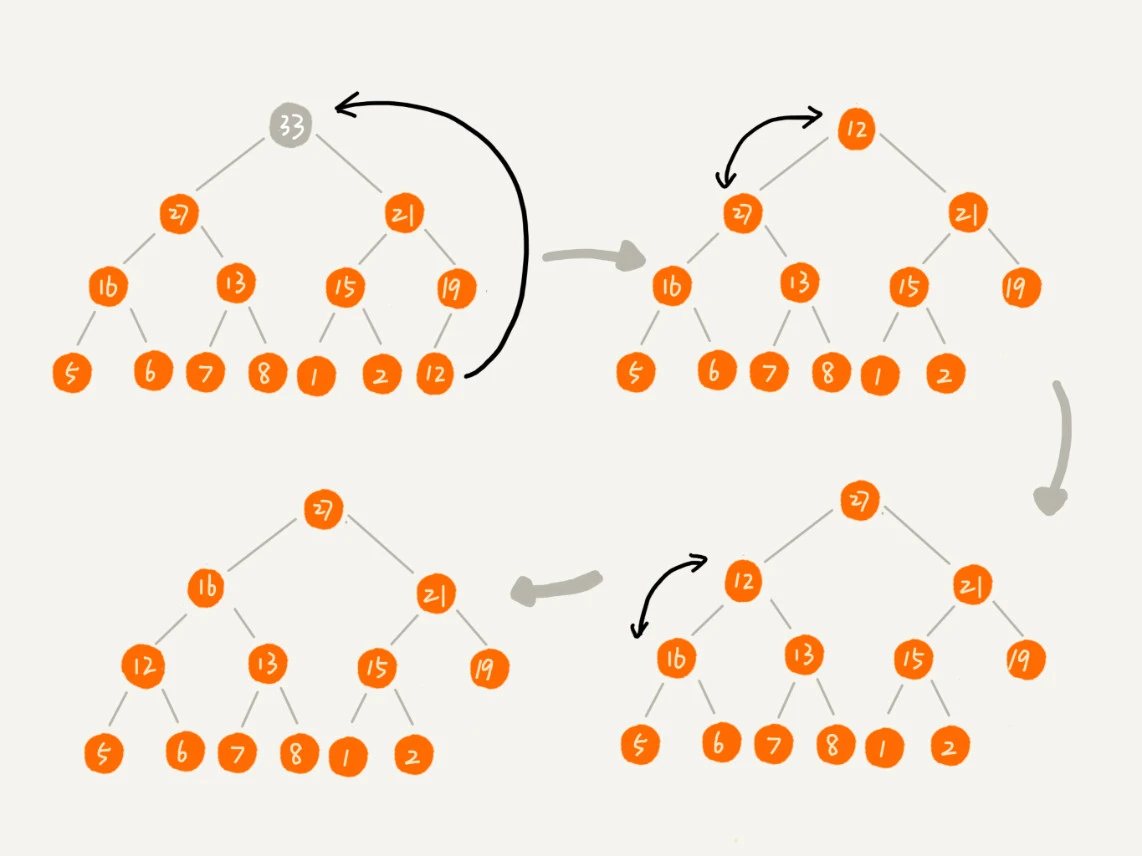
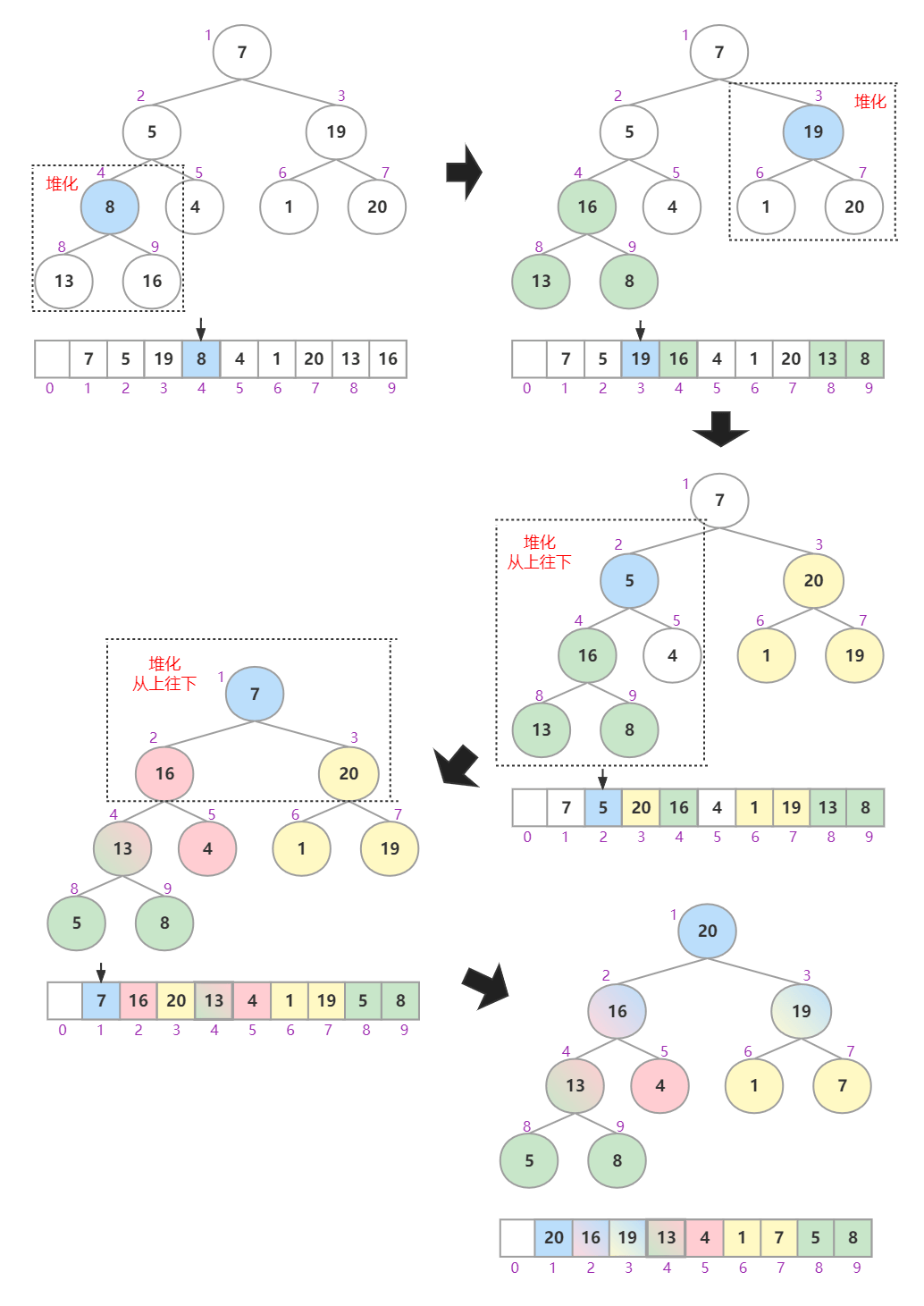
这里提供一种构建思路：从最后一个非叶子节点开始从后往前处理数组，并且每个数据都是从上往下堆化。

包含 n 个节点的完全二叉树来说，下标从 2/n+1 到 n 的节点都是叶子节点；我们对下标从 2/n 开始到 1 的节点（非叶子节点）开始处理数组。

如下图，9个节点，从数组下标4开始处理数组，构建大顶堆。

实现代码：

private static void buildHeap(int[] a, int n) {
  for (int i = n/2; i >= 1; --i) {
    heapify(a, n, i);
  }
}
private static void heapify(int[] a, int n, int i) {
  while (true) {
    int maxPos = i;
    if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;
    if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;
    if (maxPos == i) break;
    swap(a, i, maxPos);
    i = maxPos;
  }
}

堆排序的建堆过程的时间复杂度是 O(n)。

每个节点堆化的时间复杂度是 O(logn)，因为叶子节点不需要堆化，所以需要堆化的节点从倒数第二层开始。
每个节点堆化的过程中，需要比较和交换的节点个数，跟这个节点的高度成正比。通过将每个非叶子节点的高度求和，最终求得建堆的时间复杂度就是 O(n)。

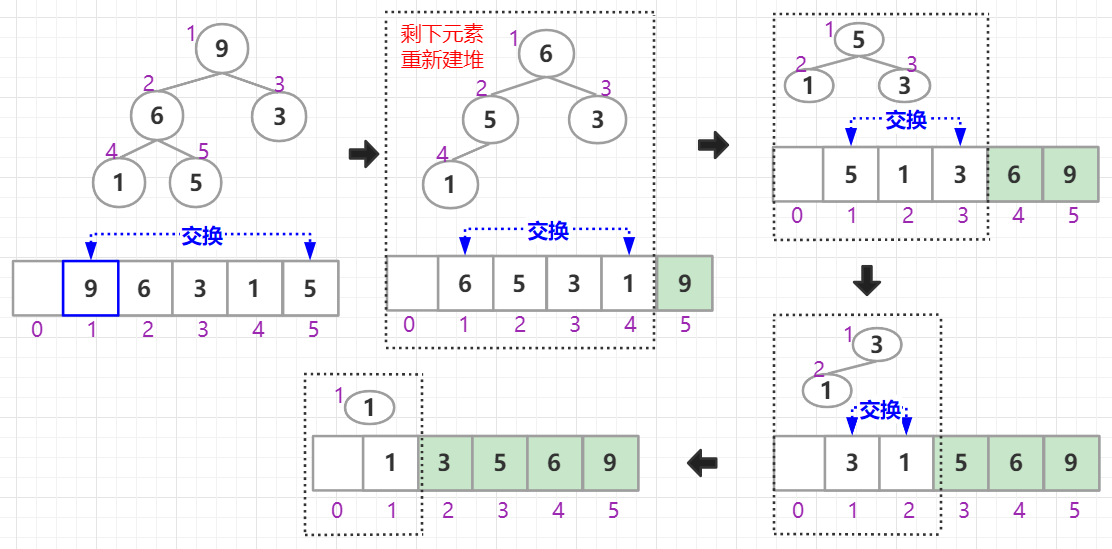
3.2 排序

建堆结束之后，数组中的第一个元素就是堆顶，大顶堆的堆顶也就是最大的元素。我们把它跟最后一个元素交换，那最大元素就放到了下标为 n 的位置。剩下 n-1 个元素重复这个过程(堆化->取堆顶)。一直重复，直到最后堆中只剩下标为 1 的一个元素，排序工作就完成了。

堆排序的过程代码：

// n表示数据的个数，数组a中的数据从下标1到n的位置。
public static void sort(int[] a, int n) {
  buildHeap(a, n);
  int k = n;
  while (k > 1) {
    swap(a, 1, k);
    --k;
    heapify(a, k, 1);
  }
}

整个堆排序的过程，都只需要极个别临时存储空间，所以堆排序是原地排序算法。
堆排序包括建堆和排序两个操作，
建堆过程的时间复杂度是 O(n)，
排序过程的时间复杂度是 O(nlogn)，
所以，堆排序整体的时间复杂度是 O(nlogn)。
堆排序不是稳定的排序算法，因为在排序的过程，存在将堆的最后一个节点跟堆顶节点互换的操作，所以就有可能改变值相同数据的原始相对顺序。

在实际开发中，为什么快速排序要比堆排序性能好？

第一点，堆排序数据访问的方式没有快速排序友好。

对于快速排序来说，数据是顺序访问的。而对于堆排序来说，数据是跳着访问的（堆化）。 CPU对于顺序访问的数据更加友好，可以做缓存。

第二点，对于同样的数据，在排序过程中，堆排序算法的数据交换次数要多于快速排序。

堆排序的第一步是建堆，建堆的过程会打乱数据原有的相对先后顺序，导致原数据的有序度降低。

4. 堆的应用

4.1 优先级队列

在优先级队列中，数据的出队顺序不是先进先出，而是按照优先级来，优先级最高的，最先出队。

用堆来实现是最直接、最高效的。
这是因为，堆和优先级队列非常相似。一个堆就可以看作一个优先级队列。
很多时候，它们只是概念上的区分而已。往优先级队列中插入一个元素，就相当于往堆中插入一个元素；从优先级队列中取出优先级最高的元素，就相当于取出堆顶元素。

优先级队列的应用广泛，如赫夫曼编码，图的最短路径，做小生成树的算法等。

4.2 利用堆求Top K

针对静态数据：
- 可以维护一个大小为k的小顶堆，顺序遍历数组，从数组中取出数据与堆顶元素比较。如果堆顶元素大，就将堆顶元素删除，并且将这个元素插入到堆中；如果比堆顶元素小则不做处理，继续遍历数组。这样等数组中的数据都遍历完之后，堆中的数据就是前k大数据了。
- 遍历数据需要O(n)的时间复杂度，一次堆化操作需要O(logk)的时间复杂度，最坏情况下，n个元素都入堆一次，时间复杂度就是O(nlogk)。
针对动态数据：求得Topk就是实时Topk。
- 一个数据集合有两个操作，一个是添加数据，另一个询问当前的前k大数据。
- 可以维护一直都维护一个k大小的小顶堆，当有数据被添加到集合时，就那它与堆顶的元素对对比。如果比堆顶元素大，就把堆顶元素删除，并将这个元素插入到堆中，如果比堆顶元素小，这不处理。这样，无论任何时候需要查询当前的前k大数据，就都可以立刻返回给他。

4.2 利用堆求中位数

对于一组静态数据，中位数是固定的，可以先排序，第n/2个数据就是中位数。
对于动态数据集合，就无法先排序了，需要借助堆这种数据结构，我们不用排序，就可以非常高效的实现求中位数操作。

实现思路：
1. 需要维护两个堆，大顶堆中存储前半部分数据，小顶堆中存储后半部分数据，且小顶堆中的数据都大于大顶堆中的数据。
2. 如果新加入的数据小于等于大顶堆的堆顶元素，就将这个数据插入到大顶堆；否则就插入小顶堆。
3. 当两个堆中的数据量不服和中位数的约定时，就从一个堆中不停的将堆顶的元素移动到另一个堆，重新让两个堆中数据满足上面的约定。

可以利用两个堆实现动态数据集合中求中位数的操作，插入数据因为涉及堆化，所以时间复杂度变成了O(logn)，但求中位数只需要返回大顶堆的堆顶元素就可以了，所以时间复杂度就是O(1)。

原文链接: http://chaooo.github.io/2022/05/02/data-structure-heap.html

版权声明: 转载请注明出处.

秋过冬漫长

没有比脚更长的路，走过去，前面是个天！